|
AI課堂開講,就差你了! 很多人說,看了再多的文章,可是沒有人手把手地教授,還是很難真正地入門AI。為了將AI知識體系以最簡單的方式呈現給你,從這個星期開始,芯君邀請AI專業人士開設“周末學習課堂”——每周就AI學習中的一個重點問題進行深度分析,課程會分為理論篇和代碼篇,理論與實操,一個都不能少! 來,退出讓你廢寢忘食的游戲頁面,取消只有胡吃海塞的周末聚會吧。未來你與同齡人的差異,也許就從每周末的這堂AI課開啟了! 讀芯術讀者交流群,請加小編微信號:zhizhizhuji。等你。后臺回復“周末AI課堂”,查閱相關源代碼。 全文共2202字,預計學習時長6分鐘
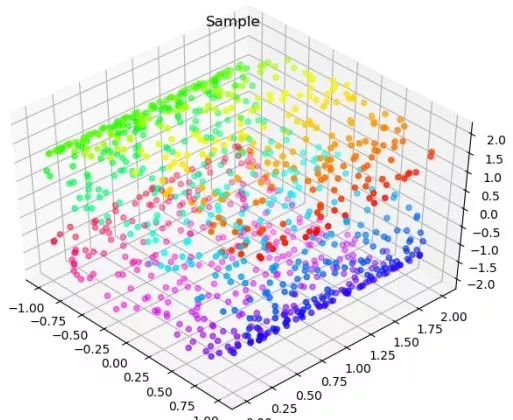
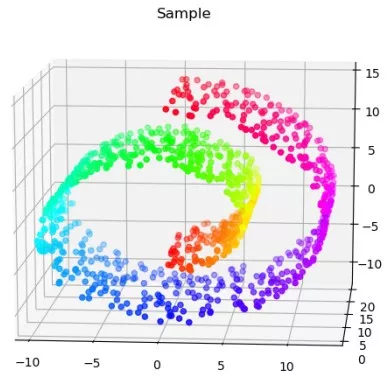
收收心,上課時間到啦。 我們在上周的《線性降維方法(代碼篇)》中對IRIS數據和WINE數據利用了PCA和LDA這兩種線性降維方法,似乎取得了一定的效果,一方面體現在低維空間不同類的樣本分的足夠開,另一方面體現在經過降維后,分類器的表現更好了。 而非線性降維的一個重要前提就是,數據的分布本身就不是高維的,而是一個嵌在高維空間的低維流形,而這樣的低維我們可能只需要將其展開,而不需要將其變換。比如,地球表面近似為一個球面,球面上的我們對球面的感受不會是三維的,而是二維的,但卻不得不用三維的語言去描述它而已。如果我們想研究它的內在結構,可能只需要將其展開為二維。我們將其展開的過程,就是降維。 我們在IRIS和WINE的數據里很難發現這樣的結構,一方面因為實際數據中完美的流形并不存在,另一方面因為,我們最多只能在三維空間可視化,而特征數一旦巨大,我們通過特征的組合去觀察每一個三維空間的數據結構,將是不可能的任務。 但我們可以通過非線性降維的方法,來逆推整個結構,如果我們的非線性降維取得了比線性降維的更好的效果,那么很可能本身的數據就是一個低維流形。 我們可以構造一個簡單的樣例數據,來可視化一個二維流形: import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3Dfrom sklearn import datasetsX, c = datasets.samples_generator.make_s_curve(1000, random_state=2018)ax = Axes3D(plt.figure())ax.scatter(X[:,0],X[:,1],X[:,2],c=c,cmap=plt.cm.hsv)plt.title('Sample')plt.show()
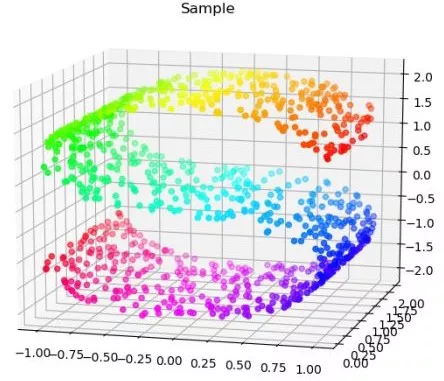
從這個角度看,平平無奇,但我們換個角度來看它:
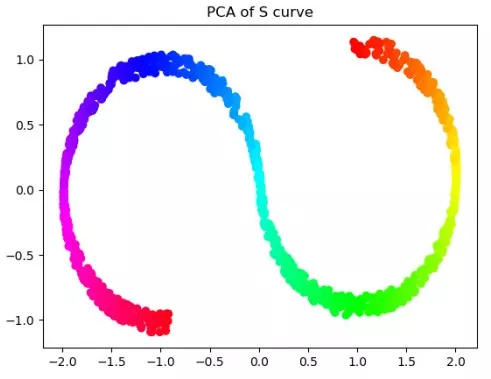
對于這樣一個S形,其實就是嵌在三維空間的二維流形,我們如果要從三維降到二維,非線性降維只是將其展開,會盡可能保持流形的內在結構,而數據分布本身近似為流形,內在結構就非常重要。 以PCA和ISOMAP為例,我們分別對樣例數據做降維: from sklearn.decomposition import PCA X_PCA=PCA(2).fit(X).transform(X)
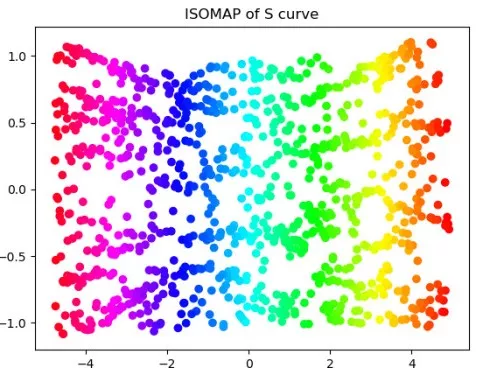
from sklearn.manifold import Isomap X_ISO=Isomap(10,2).fit(X).transform(X)
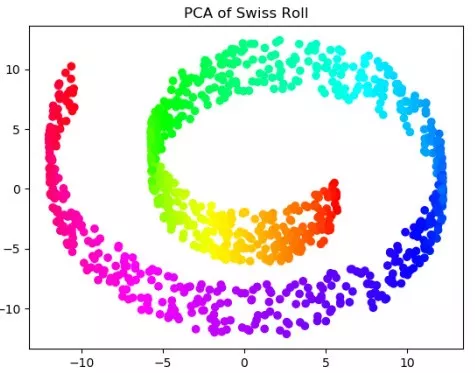
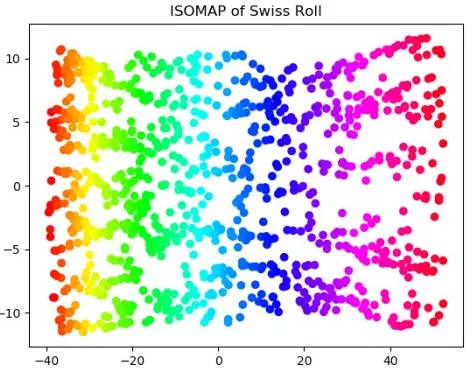
PCA的降維結果是一個S形,其實近似于一個嵌在二維空間的一維流形。很多初學者或者不理解降維的意義的同學,反而會以為PCA處理之后,樣例數據保持了S形,就是一個好的處理。 其實呢,這樣的看法是錯誤的。因為對于這樣一個三維空間的二維流形,因為流形本身就是二維的,我們只需要將其“展開”和“鋪平”,這樣才最大程度上保留了信息,PCA這種線性的降維方式只是選取了一個投影空間,大量的樣本在低維空間沒有得到表達。 舉個不太恰當的例子,如果我們把國家作為我們的數據點,那么這些數據點就分布地球表面,也就是一個嵌在三維空間的二維流形上。如果我們為球面尋找一個低維空間,PCA會把球面映射到一個圓(損失大量信息),而ISOMAP會映射成一張世界地圖。(事實上,要想達到這一效果,對地球表面的數據分布做更多的假設,但道理相同) 我們可以換另外一組數據來取得相似的效果: n_points = 1000 X, color = datasets.samples_generator.make_swiss_roll(n_points,random_state=2018)X_PCA=PCA(2).fit(X).transform(X)X_ISO=Isomap(10,2).fit(X).transform(X)ax = Axes3D(plt.figure())ax.scatter(X[:,0],X[:,1],X[:,2],\c=color,cmap=plt.cm.hsv)ax.set_title('Sample')bx=plt.figure()plt.scatter(X_PCA[:,0],X_PCA[:,1],c=color,cmap=plt.cm.hsv)plt.title('PCA of Swiss Roll')cx=plt.figure()plt.scatter(X_ISO[:,0],X_ISO[:,1],c=color,cmap=plt.cm.hsv)plt.title('ISOMAP of Swiss Roll')plt.show()
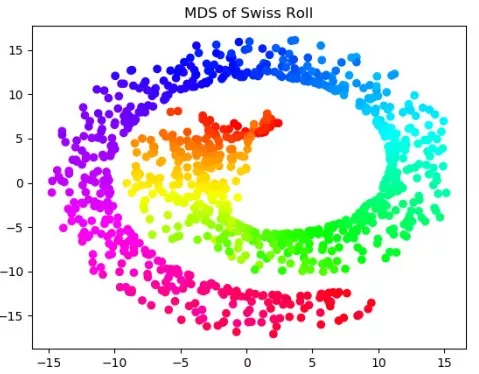
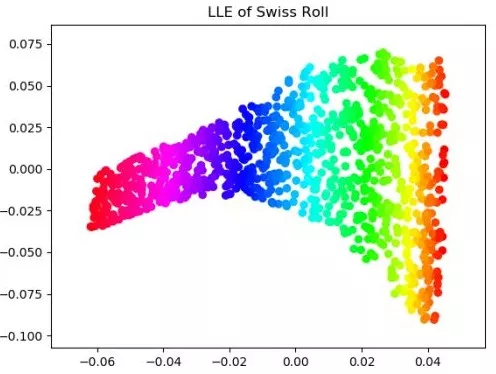
我們嘗試用更多的方法如MDS和LLE(locally linear embedding,局部線性嵌入),對swiss roll數據進行降維:
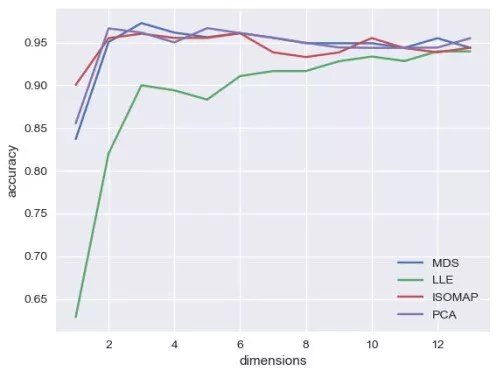
值得注意的是,MDS(多維縮放)本質上還是一個線性算法,雖然它的初衷是在低維空間保持高維空間的距離,但仍然把歐幾里得距離作為度量,所以從圖中來看,MDS的效果幾乎與PCA的一致。而LLE是利用了流形的局部等價于歐氏空間,每一個點都可以被周圍的點進行線性表示(這也是線性空間的性質),降到低維空間后,要保持擬合系數的不變。 接下來,我們把非線性降維方法用到實際的數據中,我們在WINE數據上,對線性降維和非線性降維方法進行對比:以低維空間的維度作為超參數,仍然選取k-近鄰作為分類器,通過觀察測試集上表現來對降維效果有定性的認識。 import numpy as np from sklearn import datasetsfrom sklearn.model_selection import cross_validatefrom sklearn.manifold import Isomap,MDSfrom sklearn.manifold import locally_linear_embedding as LLEfrom sklearn.decomposition import PCAfrom sklearn.preprocessing import StandardScalerfrom sklearn.neighbors import KNeighborsClassifier as KNCimport seaborn as snsimport matplotlib.pyplot as pltdata=datasets.load_wine()X=StandardScaler().fit(data['data']).transform(data['data'])y=data['target']def dim_reductor(n,X):reductor=dict(PCA=PCA(n).fit(X).transform(X),\ISOMAP=Isomap(10,n).fit(X).transform(X),\MDS=MDS(n).fit_transform(X),\LLE=LLE(X,10,n)[0])return(reductor)mse_mat=np.zeros((4,X.shape[1]))for nin range(1,X.shape[1]+1):reductor=dim_reductor(n,X)test_mse=[]for name, methodin reductor.items():X_new=reductor[name]clf=KNC()clf_dict=cross_validate(clf,X_new,y,\ cv=5,scoring='accuracy')test_mse.append(clf_dict['test_score'].mean())mse_mat[:,n-1]=test_msesns.set(style='darkgrid')for idex,namein enumerate(reductor.keys()):plt.plot(range(1,X.shape[1]+1),mse_mat[idex],label=name)plt.xlabel('dimensions')plt.ylabel('accuracy')plt.legend()plt.show()
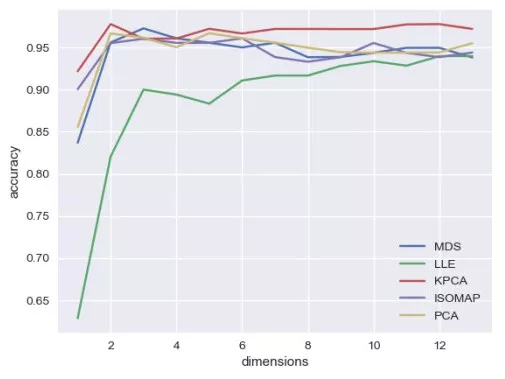
我們發現,無論在哪一個維度,LLE的表現均是最差的,而且LLE并不會隨著維度波動,而是一直在上升。而其他三種降維方法,MDS在維度為3的時候表現最好,PCA在維度為5的時候表現最好,ISOMAP在維度為6的時候表現最好。這能否說明,WINE數據并沒有明顯的流形結構,或者ISOMAP的結果告訴我們,WINE數據其實可能是一個嵌在13維空間的6維流形,這些我們無從得知。從工程上來說,我們可能需要將各類流形學習用進去,直到降低合適維度可以得到我們需要的性能。 這些算法看起來并沒有太大的差異,我們也可以看到MDS,ISOMAP,PCA三種方法交纏在一起,難分高下,那么我們大膽地來試一種雖然不屬于流形學習,但卻屬于非線性降維——加了kernel的PCA: from sklearn.decomposition import KernelPCA def dim_reductor(n,X):...KPCA=KernelPCA(n,'rbf').fit_transform(X)#添加到前文的dim_reductor函數中.........
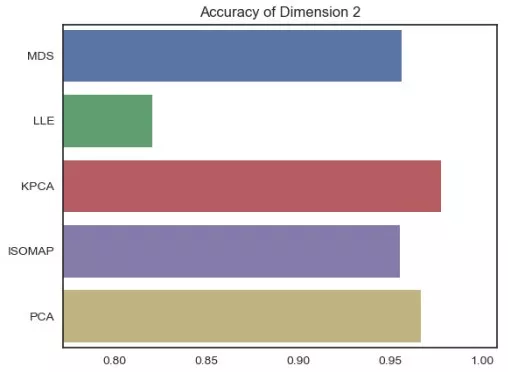
我們驚奇地發現,Kernel PCA的曲線幾乎一直在其他曲線的上方!這說明,在幾乎所有的維度上,Kernel PCA的表現要好于其他的降維算法(針對WINE數據),維度等于2時,我們還可以比較各類降維的算法的表現: sns.barplot(mse_mat[:,1],list(reductor.keys()))
那么為什么PCA加了Kernel,性能就要比原始的PCA算法更好呢?以及,Kernel到底是什么?為什么會加了Kernel就使得PCA從一個線性算法變成了非線性?下周我們再見吧,《機器學習的核技巧(kernel trick)》會為大家來解答。
讀芯君開扒 課堂TIPS ?當數據處在一個高維空間的低維流形時,我們就可以方便的使用內稟坐標,即流形中的坐標就可以很好的描述數據,流形學習的出發點就在于此。 ?流形學習除了ISOMAP和LLE,常見的流形學習方法還有 Hessian Eigenmapping,t-SNE, Laplacian Eigenmaps ,Local tangent space alignment。但流形學習需要克服最大的問題在于,流形的局部空間等價于歐氏空間,而在局部往往就要進行密采樣的操作,而這一條件往往得不到滿足。 ?特征選擇和降維本身雖然并不相同,但也并不矛盾,我們在實際工程中,可以先做特征選擇,再做降維,對于不同的數據,可能會有不同的效果。但可以預見的是,當存在多余特征的時候,高維空間的點會變得更加稀疏,密采樣會遇到更大的困難,先做特征選擇去除掉多余特征是非常有必要的。
留言 點贊 發個朋友圈 我們一起探討AI落地的最后一公里 作者:唐僧不用海飛絲 如需轉載,請后臺留言,遵守轉載規范 |
- 關注天氣: